離線返馳轉換器回授設計

Feedback Control Design of Off-line Flyback Converter

摘要

離線返馳轉換器 (off-line flyback converter) 的回授控制經常困擾著電源工程師，因為牽涉到連續導通模式 (continuous conduction mode, CCM) 與非連續導通模式 (discontinuous conduction mode, DCM) 的小信號模型，TL431 與光耦合器 (opto-coupler) 的特殊回授補償模式，使得回授參數的設計，還流於試誤 (cut and try) 模式。本設計指南就理論設計的完整度，從功率級的轉換函數，到設計TL431與光耦補償器，使得系統獲得良好的相位裕度 (phase margin)，達到暫態穩定度的要求。本文將利用 Mathcad 軟體做理論計算，同時以 Simplis 模擬做比較驗證。此法將可應用在立錡科技 RT773x 離線返馳控制 IC 的電路設計。

一、適用範圍 : 次級穩壓返馳轉換器

絕大部份返馳轉換器都採用次級穩壓的峰值電流控制 (peak current mode control) 來完成調節輸出電壓的回授方式。圖一為其簡圖。次級輸出電壓經過光耦與 TL431 電路，在初級側形成電壓 V_COMP，這個電壓與初級峰值電流比較，決定開關晶體 Q 的工作週期 (duty cycle)，完成負回授穩壓的作用。其中，R_S 為初級電流檢測電阻，CTR 為光耦的電流傳遞比 (current transfer ratio)，G_FB 為小信號增益 (在RT773x IC 內部設計為1/3)，S_e 為消除次諧波振盪 (sub-harmonic oscillation) 所外加的斜率補償 (slop compensation)。

為方便後續的推導與說明，電路做了基本的假設如下：

1.開關器件Q 與次級二極體D 為理想元件

2.變壓器視為理想器件

3.TL431 的開迴路增益為無限大 (常規的開迴路增益約 50 ~ 60 dB)

4.光耦的電流傳遞比為一常數

其中，光耦的電流傳遞比是一個極非線性的數值，隨著工作點 (通過光耦二極體的電流) 的變動，電流傳遞比也會隨著變化。但為了方便說明與推導起見，姑且將其視為定值。在常規的應用中，流過光耦二極體的電流很低，可能低於 1mA，導致電流傳遞比可能小於 20%。

其他名詞與符號定義如下：

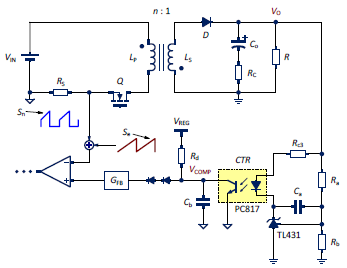
圖一、利用 TL431 與光耦回授的返馳轉換器

二、功率電路的小信號模型

在許多不同的參考文獻中可以找到不同的返馳轉換器小信號模型[1-3]，這些模型都是基於狀態平均 (state averaging) 法推導的，可能是因為簡化或假設條件不同而有些許差異。本文乃採用 Christophe Basso 的小信號模型作回授補償設計 [1]。從實用的角度而言，所有小信號模型都將得到近似的結果。

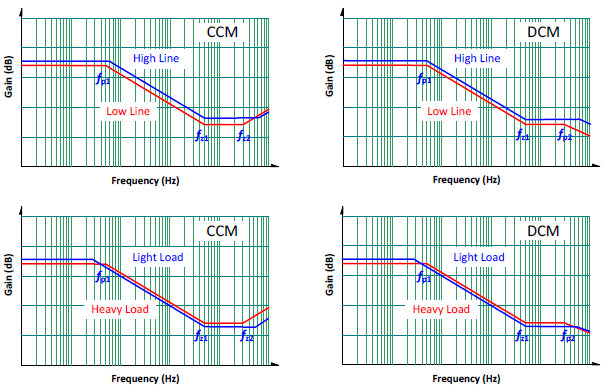
連續導通模式 (CCM) 的轉移函數 (transfer function)

這是一個一個極點 (pole) 兩個零點 (zero) 的系統，如圖二。極點的位置與電路參數以及負載輕重有關。而第一個零點為輸出電容與其等效串聯電阻 (ESR) 所構成，為一固定不動的零點。另一個零點在 s-平面的右半邊，稱為右半平面零點 (RHP zero)。這個右半平面零點的位置與輸入電壓、負載電流的高低有關。在一個設計良好的系統裡，交越頻率 (cross-over frequency) 必須設計得遠低於右半平面零點頻率，才能有足夠的相位裕量 (phase margin)。所以在補償電路設計時，這個高頻的零點將忽略不計。

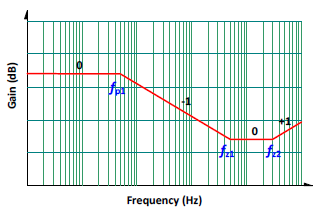
圖二、CCM 1P2Z 的轉移函數圖

非連續導通模式 (DCM) 的轉移函數

將 (2) 式的轉移函數繪製在波德圖 (Bode Plot) 上，如圖三。在 DCM 模式下，功率電路小信號模型呈現兩極點與兩零點。不過其中有一個極點頻率, ωp2 極高 (遠高於目標的交越頻率)，在設計回授時不需考慮。所以等效上，不論CCM 或是 DCM，其功率級的轉移函數，均可視為一極點兩零點 (1P2Z) 的形式，這非常有利於回授組態電路的選定。從 (1) 與 (2) 轉移函數來看，這些極點與零點，有些是固定不變的，如輸出電容等效串聯電阻 ESR 造成的零點。大部份的極零點與直流增益都與工作點 (operating point) 有關。所謂工作點即指某一個輸入電壓與某個負載電流工作條件下。接下來，就用數值來說明這些極零點的變化。

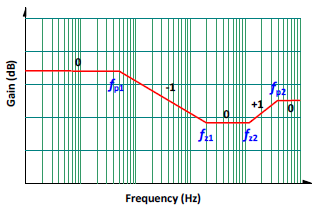
圖三、DCM 2P2Z 的轉移函數圖

工作點與極零點變化

舉一個常規的應用例子來說明。一個返馳轉換器，輸入電壓範圍為 90V 到 360V，負載範為為 0 到 3A，輸出電壓為 12V。並有著下列的電路參數 : L_P = 1.1mH, N_P : N_S = n = 7.7, C_O = 1360μF, R_ESR = 30mΩ, R_S = 0.56Ω, f_S = 65kHz, S_e = 3.46 x 104 V/sec, G_FB = 0.3333。(其中 S_e 與G_FB 必須由控制 IC 提供)根據返馳轉換器的工作原理 [4]，在常規的設計裡，高輸入電壓與輕載，總是讓轉換器傾向非連續導通模式；反之，低輸入電壓與重載的條件下，轉換器會走向連續導通模式。其間存在著一條所謂 CCM 與 DCM 的邊界曲線，如圖四所示。在曲線上方者為CCM 工作模式；曲線下方者為 DCM 工作模示。(3) 式就是代表這條曲線的方程式。

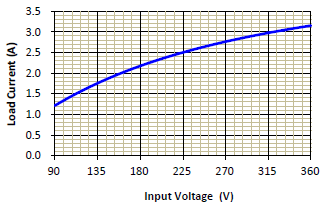
圖四、CCM 與DCM 邊界曲線

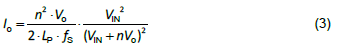
不同操作點的零極點變化

表一為計算出範例中的直流增益以及零極點位置。圖五為輸入電壓與負載電流變化的波德示意圖。可以看出，當低輸入電壓與高負載時，增益曲線較低；反之，高輸入電壓與輕載時，增益曲線較高。這個事實關係到如何選擇工作點作為回授設計的基準。很顯然的，低輸入電壓與重載條件做為回授設計點是比較恰當的。也就是說在這樣的條件下，如果擁有足夠的相位裕量，通常也能延伸到其他工作點有著更好的相對穩定裕量。

表一、不同工做點的直流增益與零極點位置

圖五、改變工作點的增益曲線變化

三、回授補償電路設計

從前面的分析得知，不同的操作點有著不同的零極點位置，以及不同的低頻直流增益，所以存在著許多設計補償電路的方法。基本上一個 Type II 的補償器 (一個零頻率的極點，隨著一個低頻零點，以及一個極點) 最適合做此類的補償。如果用一個低頻零點來補償功律電路的低頻極點，同時利用高頻極點來補償 ESR 零點，這樣將容易獲得較好的相位裕量。利用補償器的中頻段增益來設定適當的交越頻率，系統將有相當好的穩定度。一種簡單實用的方法便是先設定好一個 ”目標迴路增益” (target loop gain) 為：

這樣的迴路增益在波德圖上就是一條 -20dB/dec 斜率的直線，如圖六。在低頻直流部分有著極高 (相當於補償器的開迴路增益) 的增益，所以整個電路的直流穩態電壓調整率理論值可為零。同時，其交越頻率，f_C 為

因為斜率近似 -20dB/dec，所以在交越頻率有著近 90° 的相位裕量。對一個離線的返馳轉換器而言，交越頻率設計在低壓輸入滿載時工作點為 800Hz 到 3kHz 為最恰當 (以 65kHz 開關頻率而言)。

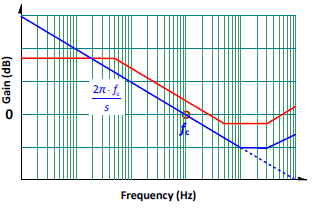
圖六、功率電路轉移函數曲線(紅色)與目標迴路增益(藍色)

設計步驟

有了以上的瞭解與認知後，很自然的一般補償器設計的方法就可以應用了。將這些步驟整理如下 :

1.選擇低壓輸入與滿載做為補償電路設計基準的功率電路。如前所述，採用這個工作點設計的補償器可以延伸涵蓋到其他工作點有更好的相位裕量。

2.設定交越頻率 f_C，其迴路增益波德圖為 -20dB/dec 斜率。越高的交越頻率，雖然代表著更快的暫態響應，但是別忘了返馳轉換器固有的右半平面零點問題。這個零點無法用傳統的極點補償。所以交越頻率必須遠低於這個零點位置。實務上，離線返馳轉換器的交越頻率多半設計在3kHz 以下。

3.定義一個兩極點一零點的補償電路，並設定補償電路的零點為功率電路的低頻極點；設定補償電路的高頻極點為功率電路的 ESR 零點。利用一組 Type II 的補償電路，恰可以結合功率電路的轉移函數，成為目標迴路增益。

4.根據功率電路在 f_C 的增益，算出補償器的中頻增益。

5.同時，相位裕量可以先預估。

6.補償電路的轉換函數可以確定。

也就是說 (6) 式的 A、ω_cp1 與 ω_cz1 都可以計算出來了。

補償電路的實現

1.選用最廣泛使用的TL431與光耦合器架構，如圖七。實現Type II 補償器的電路結構有許多種，不在此討論。僅提供最常用結合TL431與光耦的常規Type II電路計算與說明。

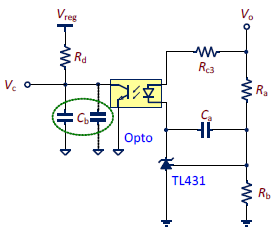
圖七、實現回授補償的電路結構

2.圖七補償電路的小信號轉換函數如下 [5]：

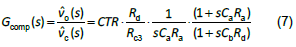
圖八為相應的補償器波德圖。

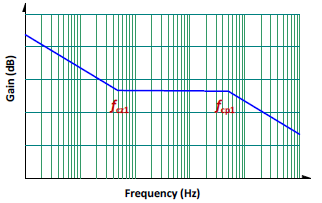
圖八、Type II 補償器波德圖

3.從 (7) 式看，共有 R_a、R_b、R_c3、R_d、C_a、C_b 及 CTR 等七個參數待定。而已知的只有前面算出的三個關係式。

換句話說，有四個參數必須從其他條件獲得。

4.首先為電阻R_d，大部份新型的控制 IC 都已設定好，設計者可以從 IC 供應商資料中獲得。

5.其次，TL431 的參考電壓也可從供應商資料中得取，常規約為 2.5V。為讓 TL431 正常運作，通過 R_b 的電流 (I_vd) 至少須 125μA，一般加上餘裕，可以設定成 250μA。所以 R_a 與 R_b 就可以很容易的計算出來。

6.此外，光耦的電流傳遞比 (CTR) 可以從供應商資料裡估計。事實上如前所述，CTR 為一非線性值，隨通過光耦二極體電流大小而變。一般通過光耦二極體電流約為幾百 μA，CTR 約在 0.1 到 0.5 之間。確實的數值必須透過精密量測而得。此例將假設 CTR 為 0.5。

7.如此一來，七個參數已經決定了四個，其餘的三個參數可藉由 (8)、(9) 及 (10) 三個關係式算出唯一解。

8.算出R_C3 的數值後必須要檢討一下。從 TL431 運行原理，其陰極電壓必須高於 2.5V，同時流過陰極的電流必須大於 1mA 才可以獲得正確的穩壓。通常會在光耦二極體上並聯一個 1kΩ 左右的電阻以提供足夠的陰極電流。特別注意，這個並聯電阻並不會改變系統小信號特性。所以可以得到下列關係式:

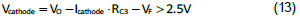
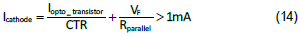
其中V_F 為光耦二極體的順向壓降，常規約略為1.0V。R_C3 的最大值就可以估計出來了。

代入前面的例子，同時假定最大陰極電流為1.5mA，則 R_C3 必須小於5.6kΩ。太高的 R_C3 會降低補償電路的中頻增益。如果計算出來的 R_C3 大於上限值就表示必須降低設定交越頻率，或採用其他的補償計算方法。

9.光耦合器在先天上存在一個並聯於光耦三極管的等效電容，必須用電路量測的方法測得，常規約在 2nF 到5nF 之間。補償器計算出來的 C_b 值必須減去這個雜散電容，才是要外加的電容值。如果算出來的C_b 值比雜散電容小，那就不需要外加電容了，不過因為不能完全補償ESR 零點(極點靠近低頻)，所以相位裕量會變差一些。

設計工具與模擬驗證

為了讓上述計算可以快速進行，特別製作兩個 Mathcad 計算程序 ”Flyback CCM Type II Compensation” 與 ”Flyback Loop Gain Analysis”，方便回授的計算與分析。同時可藉由 Simplis 模擬來比較本文模型計算的誤差。圖九為 Simplis 模擬電路圖，圖十到圖十二為本文提供的設計方法用 Mathcad 分析計算與 Simplis 模擬結果比較。圖十為功率電路轉移函數波德圖，圖十一為補償器電路轉移函數波德圖，圖十二為迴路增益波德圖。 (a) 為大小量 (magnitude)，(b) 為相位。圖中紅色實曲線為 Mathcad 依據小信號模型計算結果，藍色虛曲線為用Simplis 直接模擬的結果。可以看出從低頻段到交越頻率，小信號模型有很好的準確度。高頻部份由於小信號模型的誤差，有比較大的誤差，不過因為迴路增益已遠小於 1，對於實際暫態響應影響不大。圖十三為用 Simplis 模擬在輸入電壓為 90V 情況下步階負載變化 (負載自 1A 瞬變到 3A) 的輸出電壓暫態響應圖。可以看出只有很小的超越量 (overshoot) 以及很快的回復時間 (settling time)。

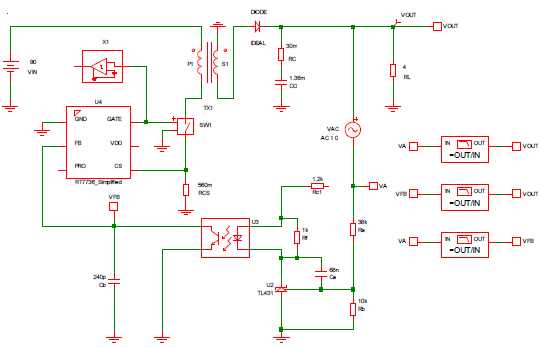
圖九、Simplis 模擬電路圖

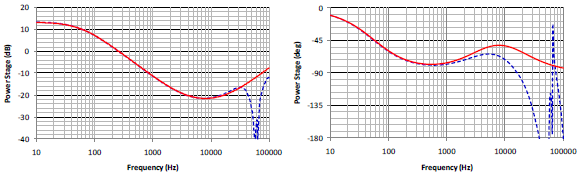
圖十、功率電路轉移函數波德圖 (a) 大小量, (b) 相位

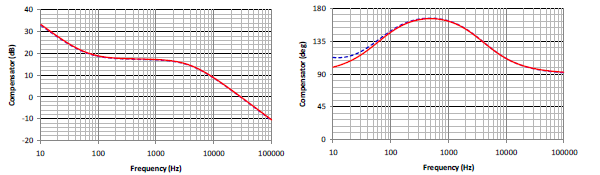
圖十一、補償器電路轉移函數波德圖 (a) 大小量, (b) 相位

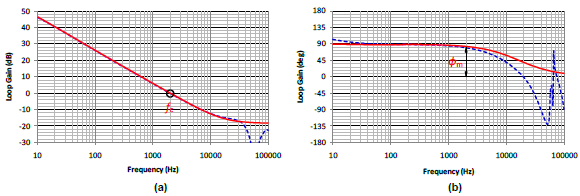
圖十二、迴路增益波德圖 (a) 大小量, (b) 相位

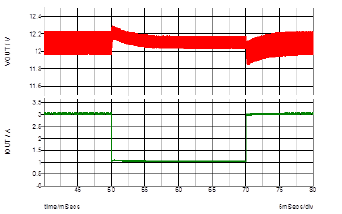
圖十三、負載瞬變暫態響應圖

參考文獻

[1] Christophe P. Basso, “Switch-Mode Power Supplies Spice Simulations and Practical Designs”, McGraw_Hill, 2008.
[2] W. Kleebchampee and C. Bunlaksananusorn, “Modeling and Control Design of a Current-Mode Controlled Flyback Converter

with Optocoupler Feedback”, IEEE PEDS 2005.

[3] Yuri Panov and Milan M. Jovanovic´, “Small-Signal Analysis and Control Design of Isolated Power Supplies with Optocoupler

Feedback”, IEEE TRANSACTIONS ON POWER ELECTRONICS, JULY 2005.

[4] 王信雄, “定頻返馳式轉換器設計指南”, RTAD1202TC, 立錡科技設計指南, 2012.

[5] John Schönberger, ”Design of a TL431-Based Controller for a Flyback Converter”, Plexim GmbH.